Reverb Part 1—“Freeverb”

Thursday, June 05, 2025

#audio #dsp #maxmsp #plugin #reverb #schroeder

All posts in this series: Part 1, Part 2

I started work on a reverb plugin in C++/JUCE back in 2023, and I've slowly added to it since. Today, I'm going to discuss how algorithmic (i.e., delay-based) reverbs work using the “Freeverb” algorithm that's available in that plugin. I've included a Max/MSP version of the reverb, and in a later post, I will discuss getting our hands dirty with the code in C++/JUCE, as well as a number of other cool algorithms. Let's get started!

How Reverb Works

There are two main categories of digital reverb—convolution and algorithmic—and today we will be discussing algorithmic reverb. An algorithmic reverb is based on a network of delays or “echoes,” with individual delays roughly corresponding to the sound reflections from individual walls or objects, and the network of connections between them simulating the way a reflection from one surface may bounce off many others.

Sean Costello of Valhalla DSP has a series of posts giving helpful resources on reverb design, including influential papers, online resources, and books, and you can find the type of algorithm we'll discuss today among the papers he mentions.

Feedforward and Feedback Delays

In the most basic form of delay, we take a copy of the incoming audio signal, delay it by a certain amount, and combine it with the original signal, usually with the option to adjust the proportions of original and delayed copies. To contrast with the other types of delay, this is often referred to as a “feedforward” delay—the delayed copy is “fed forward” and recombined with the original without any “feedback,” which we will discuss in the next section.

In the diagram below, $x (n)$ represents the incoming signal; $z^{- M}$ is the delay block (with $M$ representing the amount of delay in samples); ^[1] $b_{0}$ and $b_{M}$ represent the amount of gain applied to the original and delayed copies respectively; ^[2] the $+$ symbol represents summing the two copies; and $y (n)$ is the output signal.

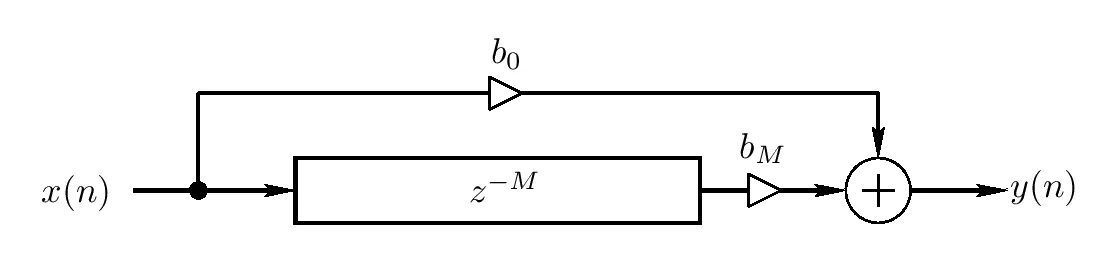
block diagram of a feedforward delay/comb filter — Feedforward delay/comb filter (diagram from Julius O. Smith)

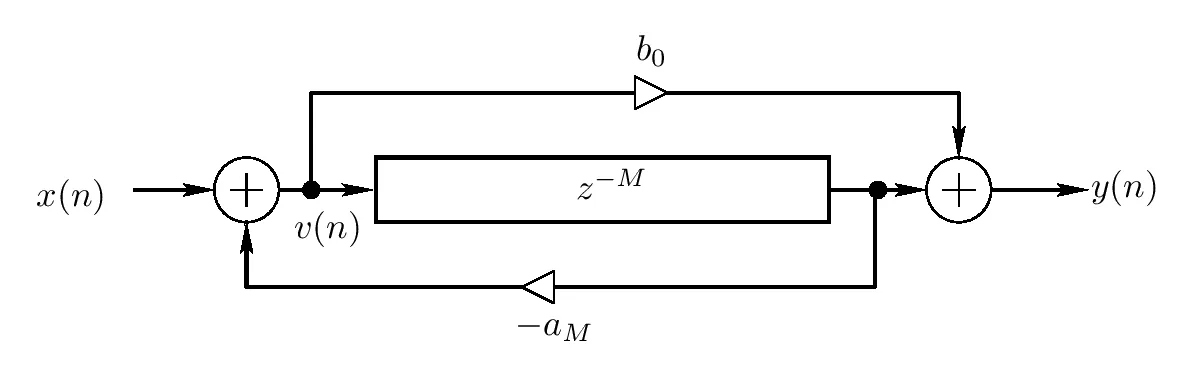
Next, we have a “feedback” delay. Note how in the diagram below, the incoming signal is summed with the fed-back output of the delay before entering the delay; the gain $- a_{M}$ applied to the fed-back output of the delay is negative; and the output of the whole delay $y (n)$ is taken from that sum of the input and feedback before it enters the delay.

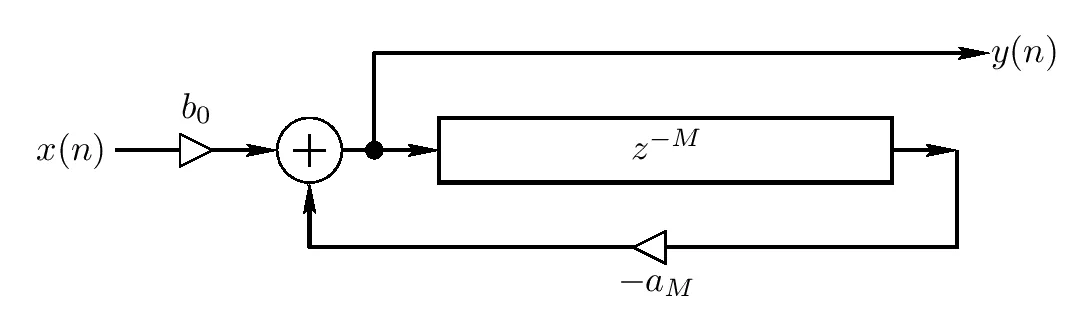
block diagram of a feedback delay/comb filter — Feedback delay/comb filter (diagram from Julius O. Smith)

Allpass Filters

Below I have the amplitude curves from feedforward and feedback delays, caused by constructive and destructive interference. The repeated notches in the feedforward delay frequency plot are caused by destructive interference; adding the delay to the original signal causes certain frequencies to cancel out. In the feedback example, as the sound feeds back on itself, certain frequencies constructively interfere—they reinforce each other and create the “spikes” in the amplitude response. Both of these delay configurations are also referred to as “comb filters,” due to the shape of the spikes and notches.

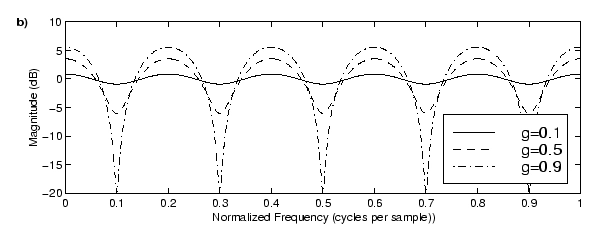
feedforward comb filter amplitude plot — Feedforward comb filter amplitude plot (diagram from Julius O. Smith)

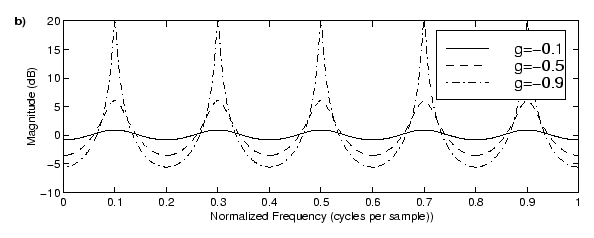
negative feedback comb filter amplitude plot — Negative feedback comb filter amplitude plot (diagram from Julius O. Smith)

Notice how the feedforward and feedback amplitude responses are the inverse of each other. Having a negative gain in the feedback loop of a feedback delay is necessary for the peaks to align with where the troughs would be in a feedforward delay that has the same delay time. As shown here, if the feedback delay's gain were positive, the peaks would be at 0.2, 0.4, etc., instead of 0.1, 0.3, etc.

This alignment is important for our next type of filter: the “allpass” filter. As shown below, we combine a feedforward delay with a feedback delay that has a negative gain on the feedback. As a result, our peaks and troughs in the frequency response cancel out. This kind of delay configuration has a “flat” frequency response; all frequencies pass through at the same loudness.

block diagram of an allpass filter — Allpass filter (diagram from Julius O. Smith)

In contrast to the frequency response, our time response is much more complex. An allpass filter delays the different frequencies in the signal by different amounts. As a result, a single impulse or “click” going through it would become multiplied and “smeared” in time, giving the effect of multiple clicks piling on top of each other, a very useful effect for creating a smooth- and dense-sounding reverb.

Now let's put these all together to make a reverb!

The Classic Schroeder Reverberator

Series Allpasses

Manfred Schroeder has two papers from 1961 that introduce the idea of allpasses and using them for reverberators.

In “Colorless” Artificial Reverberation, ^[3] Schroeder and co-author B.F. Logan note six features that they seek from a delay-based reverberator:

There should be a flat frequency response
Normal modes (i.e., resonant emphases on specific frequencies) “must overlap and cover the entire audio frequency range”
Different frequencies should decay at the same or similar rate
There should be high echo density within a short period after an impulse
Echoes must be non-periodic (i.e., no “flutter echoes”)
“Periodic or comb-like” frequency responses must be avoided

Below, I have an 808 drum machine clap played through a feedback comb filter. The delay is set at successively shorter lengths, from 50ms down to 5ms. Notice how at longer delay times, there is a “fluttering” tremolo effect. This is similar to the echoes with two walls directly facing each other, as in a long, narrow hall. At shorter lengths, there is an audible tone created by the repeated echoes. Both of these features are undesirable in a reverb effect.

In “Colorless” Artificial Reverberation, Schroeder and Logan propose a chain of allpass filters as an answer to this issue. The allpass filter is already better than the feedback comb at creating smooth-sounding results, and to improve on this further, the authors suggest “incommensurate” delay times. In other words, the delay times do not easily divide into each other, preventing the echoes from one allpass from lining up with another. The result of the incommensurate delay times is something more like the random tapping of rain, rather than any periodic rhythm.

On this algorithm, Sean Costello comments that

The resulting reverberator structure is a bit hard to tune, as both the reverb attack and decay are controlled by the feedforward/feedback allpass coefficient, and is less “general purpose” than the structure discussed in Schoeder’s next paper.

As Costello then mentions, some reverbs such as the Eventide Blackhole make artistic use of the weirdness of this structure. However, it would be helpful to have a more general-purpose algorithm.

Below I have a synth riff: first the dry signal, then a mix of the dry signal with a “wet” signal through 8 series allpasses. For the allpass example, I increase the feedforward/feedback parameter from about 0.1 up to 1, then back to 0.1 again.

As mentioned, this doesn't sound as natural as we'd like, as well as not being super flexible. It's a start though, and our next version will sound much nicer.

Parallel Combs into Series Allpasses

In Natural Sounding Artificial Reverberation, ^[4] Schroeder proposes the class of algorithm shown below. Feedback comb filters create a nice exponential amplitude decay (unlike the allpass chain in which, as mentioned above, both attack and decay depend on the same parameter). In response to the problem of “coloration” in the frequency spectrum, Schroeder notes that

extreme response irregularities are imperceptible when the density of peaks and valleys on the frequency scale is high enough

In other words, if we combine several feedback comb filters in parallel, the “comb teeth” in their frequency spectra will tightly “interlock,” creating what sounds like a flat frequency response.

The next problem after the feedback comb's frequency response is the “flutter” effect. Schroeder gives the goal of around 1000 echoes per second to make a “natural”-sounding reverb. Assuming 4 parallel comb filters with delays that don't easily divide into each other, but are in the neighborhood of 40ms (25 echoes per second), we get only about 100 echoes per second. Assuming (as Schroeder does) that a single allpass multiplies the number of echoes by about 3, two series allpasses after 4 parallel combs is enough to meet the minimum requirement.

DSP block diagram of 8 filtered-feedback comb filters summed in parallel, and feeding into four allpass filters in series — The “Freeverb” Schroeder reverberator (diagram from Julius O. Smith)

The combination of parallel feedback combs into series allpasses (or sometimes vice versa) is often referred to as a “Schroeder reverb.” The “Freeverb” algorithm shown above is one popular Schroeder reverb. The delays are given in samples, with the floating point values representing the delay feedback coefficients. In the combs, there are two values, and as far as I can tell, the first is the feedback coefficient, and the second is the lowpass filtering (more details in a moment).

Below I have first the dry synth riff, followed by the riff through the “Freeverb” algorithm on my algorithmic reverb plugin. This time it sounds much more natural, and if you play around with the Max patch (see below) or my plugin, there's much more flexibility.

One additional feature of this particular version is that there is a first-order (i.e., 6dB/octave) low-pass filter in the feedback loop of the combs. This causes higher frequencies to decay faster. While Schroeder and Logan seek to make all frequencies decay at an equal rate, the most important aspect seems to be to prevent individual frequency bands from ringing and standing out. Reverberations in the physical world decay more quickly at higher frequencies, due (at least in my understanding) to the sound absorbency of building materials, as well as the fact that the atmosphere can be approximated with a low-pass filter.

Some final design notes: First, we have the stereo spread. The right channel has a slightly longer delay time than the left, with a default value of 23 samples added to each delay value, according to Julius O. Smith. This simulates the effect of different physical environments to the right and left of the listener. Second, in my JUCE implementation I have a low-frequency oscillator (LFO) slowly modulating the first and third allpass filter delay times longer and shorter, giving a chorusing effect and making the sound richer.

If you want to play with this reverb algorithm in Max/MSP, you can use the patch below:

“Freeverb” Max patch. Copy code and select New From Clipboard in Max.

----------begin_max5_patcher----------
8187.3oc6c10baiikF95jeEZzbW2IYv2jb2axdeuaU6bamtbQaQ6vokk7JQm
NYlZ5e6KIAkDoD+.fBVBR5cposCIkLOmC93.f2GR7ud+6ld+xumrd5j+iI+5
j28t+06e26JOUwIdW0wua5ywe+g4wqK+XSeX4yOmrHa5GzWKK46YkmeV5iO9
55zkK1bkWhyd3qoKd5tUIOjouCBE4SjOLgJEE+RFV7SV9ol7aUemEu9b5h4I
Yk2JZ0ISmUdCVd++3ibxzcexkuls4iRJN4+98uu3Ge3Xcj3meI2r6yMHz5tg
xZ2fE916FOLO8geeR1WSWO44j0qieJYR7hYSVG+sjIYKm75KyhyRlrJ4aIqt
ex5jrrbeb8l+JySWj7vxWWT9mh0cjPpJiDBYY7PW5x41DITtKRT4lsTybU1O
lNnSDxKs9x+Mi0kOvZwGDs6CabW8ox9wKI562zoS9sQ3dKR9i761AdWQIboS
krZXejRKcRUP+NYaETr1cRVmN4GJczpKWTsq5B+0+mhK0vrmL8+r3G+0+2he
lrXl9LNHJ8s3UKhet7NO8UFgQHbNO5fXX7qYKyMlr9hf4euxHHQUqQuUQPZ6
QPQ0Y+Z5rYIK5uhyGp8eauwqRVmsbURUPoJpTdWtOO3V9M+nbmgt4J+J82zW
j1x0XUWi7o.5AWju8hxCtln90JuTYAny5bN4g39ZKyEhZcMKFQWymfLLqS+m
I83CrPUcefasOPOAoWlsJ9oxDJyVs7kIwSdLcdxj7FykIWdYduERTc4hN+OM
bDNnCyZ737k4+QZqCipFP8TPwzETg5wAPNnKgGWt543xOrxTOiu69sJ2PxRV
cWxh36mWZRjd6BN+ub5y4tR9o9Xowr0a2b5Zms09VtONebOipa2tpl7b52MH
.pqoyse7fB2UOnizq+2he4SOrZ450r+b3ZzLsiDD1exAYKk68ma3fRq0oOsH
ddQYVO+qQUR10nnV9RReCsmRXkMBDk+hKsdTTT5IYTTyS+VxmdJNcwe1VS9C
uZ2E1BYYGWTt9nfZ9Z9cK+aEuXQx7sihlXXbP0WG.zVCQRapkT7e484k2szG
J720Y6FHwxUo4sgiyJlDWsaVwX2lcWwviRu+0rjc+q06OjiuEO+0jkOt4zaN
eceIuOprzh5lkCKQsc7Cs7YNzua7ox629otK3Z7QeNuJPYuva59auqlV5ueL
fz90WNK++Wde3sb40ec4pLCMjMkMscadM2qWm8CsCKzWWO1owMDpj+4r3GLn
dbUSV8b3DRKZxJcWuuEiXnnxnA1ajdXC5zs75YKdIM+67vxUEekp5vjsYhmO
e4e7z7k2GOOK44WV1YSxM05yRy6ILaUR9expQz1Ls9hr1uS2GuN8gr7ByhTo
4EjBRKKig8I42zFeSMQ88Y5tVtOkl2.edxhmx1XuEwmb23geecsl31kHo3+l
kV5iwq9wt+L+euFOOMeR0cZHaiwT1twbLKNKd+tLdXd5KUq+zwLegNxd+Txh
+bxmyRyc5IOtJobwNFd7H7pQlRGXZxpVxhIrbZxsjztt8om.W8.Vw.syci0M
6j9cSie4kZmtY2uOG+OVV9GJba+N4tg9TpsmZUx2R278kaOa7p7nTVdH5U8T
Lm9ckXWWaEUGWs30zRSYSeVeXaYadwSQOi4yz+A8Wd15W9zSaGHQw8bSrORO
TPRY01HVYnWFwqO2z6ya+9vumLqdOnkiKIcwK4SBtdtqsWdVxiwuNO6tGWtH
qbdWk0I+TqW+wJqr0KtsG9+qUE4u17QdZU5rkKJGbT8RihSu41k2ykd8wZLI
7xOwh3WZ4KmWQJOrzwEWm6jut993UEEVUcYv1bwrkKm27Ra+dySdLq5xujlO
xjlQwrkuz8EyaS+0d9t2uL+hO22e6xqrNOCm9p2UL9n61rjP69b48eU0Nt4e
9uGmOwl3rjhtjKcWx1Kp617qqyGh974M7W8U9VKWYVd87GR9izY5dJI0qLj+
wSeYSknoaKkmk9Tx5rlmKK9o0MOy1r20N0q2W0N9thtDmm6EM+.4sPxS6kOF
h+XyxgsohV8.vtknud655cJ137804XyNHSWLgM4yUydaxWl92mj2V50ruLs9
mt0bw50YgUN1AZ0hTTqmxC6sjT6BsjKr6g926v+qMJoM4KbbHJu6pMoP9xzM
IQl72GLDwBJa0yCzcrc3BK24DCOHDcDwn8swcITZFN5LwRWIW16q2VRlNRzz
cxlgS3zURmFIdLL4ydIfnrpkHWuNubYYJnPVTyRr1SCYPpHSRGMXJICSK0Sp
IyROMPJpASSMXppARWMbJqASaYPpKSReYSJrdRiMXpr9Sm0eJs9Sq0apstRu
0dJtNRyYTpNCS20dJu86sY+90O35C0+dy93+4IL99WrUMfJ6SHhpWjKVa8n2
4LJasmc0zC+ls269fYAajIrY1PuJ5ETIzpChdxaunmpRjcGD8D2dQOovYQO9
MTziFP05aDJcU3icKE9jDgN7obT3icK01kVUsycgO5MUiWRfiq8QukZ7Fp3N
N5QughdJI0sQuaoN9DUDQ3tzF2PAOFywAuqhls+zDtfZ93kC0nrvCN91spqi
vmvlvWfHxUgO40Q3SJUVLW2J4XcP3SbcD9XLoES1kvcU36pX7x0DxId97WJ9
VFjFIpbtGQZbSnDtYASdOASGjEtM6toxNGFq5Ugm9T4ok+Tco1SOJ9zupOlo
7Sep+bfBPVnBTuJAozq1qpXfD6G46VLHCEDxTQgLRXHKDGZ.AhLWjHCDJxHw
hLRvHCDMxLgiLR7HCEPxTQjrUHoADSxHAkFVTogEVZXwkFTfo9DYpagl5QrI
iEbxBQm5V3o15.rsbSs94LIG09o4OXtFcu3DeRVznrriJVmI5GLY+fZCLbdJ
iR7ePx+CG.vINX+yFFoUxhHMORm+Op3.yhzrAhz7akH8OYXjlFETFpoDWGpo
HT2LTGTVolpIp1gQZVD59nstOXUyEygQ5fakH8rj4w+XxmeLIY18wO76Sn10
wst2DJkZdNxgB8pakPe5hIzcPhVBHpcAeUMVQMK1SFnqb4MTrmuK1u8krwjO
mGrlPx+U72KJbpl0WwicsgEMLh9gbP+KNQ5tBmaoFF0nmtpGphBFS6bhJKGq
Sfd8FBHtqL3lIuPtEaYt.QEX1R2Mcovgi1DCBiGtxJEuHVLb9nk9awm2r375
kut5gMkxapxLo8XQ9b6yRWrcAr90cI.y66wM0ONZqWYo0WLE2N9BKWMSuXpz
KTWipKX5y0H9gqIssNWUkT+v5E1Z8Q9TKFtsUqB8oXO0Vqm6Qw9xJBVWu2ar
9fwzgD4RnCI1nRBdQjFgoFSKlqSWqm1eOmN6kkoKxVucIxJFqnlabIsb5r0O
fpYSU+yxCN9p460Lu4m3xS67PZnyzNmBsyg14P6bncNzNGZmCsyg14PPWncN
zNGZmCsyg14P6bncNzNGZmCsyg14P6bncNzNGZmCsyg14P6bncNzNGZmeApc
tR+KmncNAZmCsyg14P6bncNzNGZmCsygftP6bncNzNGZmCsyg14P6bncNzNG
ZmCsyg14P6bncNzNGZmCsyg14P6bncNzN+BT6bYPjqzNmGAsyg14P6bncNzN
GZmCsyg14PPWncNzNGZmCsyg14P6bncNzNGZmCsyg14P6bncNzNGZmCsyg14
P6bncNzNGZmelzN2P0xiphVA5eczaV7GtE0eguYw+X57rjUIytay5XcW9rGu
2fHKUICqEaoQFBhfnmfKGfHbQAhfd0iUBJ.Q.fH.PD.HBdhLhr.srVRliU2h
Rfhs6Ep0BXQUJGGpifNhCfZidnsLmqiXHpi2Zcb22cxMilH+kOZb0ZNUOKMp
tKbkyzD4lQDvulmRe4peXYka8uDBmEuk2lzHrN8oEGNihd6CupKbavkb.0Vo
2nJd+kproEi4+KSsT5a8fF0ReyHB2UXDbaxFx1Qzz.MDS6VhoWMS8jqY7P2U
bDdCUbHpQCR7y4Sr9oQUZTkTdCW2b2wlCMBbgzUdAgNmrC4BgQtB3BwVoJkW
JpFYqiUrZDlIZDKeHFkfUqa+V8TZTbzkfFngVFWLVKsHQo7Y540UgFZ8Cnxp
QAP1dz0X7hQtTZgXqX39DfHpwz51WHrvVrn7IpnnQiv3olz+AmwKWKnpIKzb
pCUGIz5hx2czkPCMqiYpKEfZniIahuzLjNlN.8FiWcA26cOi05XMd+9MSw3A
DQHjtFPDF.DA.h..Q.fH.PD.HB.DA.h..Q.fH.PD.HB.DA.h..Q.fH.PD.HB
.DA.h..Q.fH.PD.HB.DA.h..Q.fH.PD.HB.DA.h..Q7H.QXblqADg..Q.fH.
PD.HB.DA.h..Q.fH.PD.HB.DA.h..Q.fH.PD.HB.DA.h..Q.fH.PD.HB.DA.
h..Q.fH.PD.HB.DA.h..Q.fH.PDOBPDhlR.GBHxASVD.h..Q.fH.PD.HB.DA
.h..Q.fH.PD.HB.DA.h..Q.fH.PD.HB.DA.h..Q.fH.PD.HB.DA.h..Q.fH.
PD.HB.DA.h..Q.fHmQ.QBIJWyGRH3CA7g.9P.eHfODvGB3CA7g.9P.eHfODv
GB3CA7g.9P.eHfODvGB3CA7g.9P.eHfODvGB3CA7g.9P.eHfODvGB3CA7g.9
P7G9PjZhPbIeHAfODvGB3CA7g.9P.eHfODvGB3CA7g.9P.eHfODvGB3CA7g.
9P.eHfODvGB3CA7g.9P.eHfODvGB3CA7g.9P.eHfODvGB3CwM7g7SEBJnLYW
jIfppMkPA0LHPn8.Ah53g.wOBfgglD.kDd8.H63Cfxqj.HWZTMPV0hnVE.4G
e.TbkD.YAAFsQPEHbb.jbkD.ELlIunjTrZizyAwunqgv2eahQc+EPzxNQ1D0
NxXW30PryE3YxCINFOSPmInybuA9B5L0yV.zYB5L2uJAny7cfNSPm4EdjFzY
dgTGGzYN5HMnyDzYdMCAEny7LF7AcldTgAnyzqJN.cldSoAnyzQBkC5LAclC
xSCnyDzYB5LclwC5Laq+CPmIny7zZ7fNSPm4IhLoHpALfnj5903QNhLoqE1L
UTSHiSTstFNK7csPloTZR3iwbb3iC1tZPMmCY6hQAbW.tK.2Ef6BvcA3t.bW
.tK.2Ef6BvcA3t.bW.tK.2Ef6BvcA3t.bW.tK.2Ef6BvcA3t.bW.tK.2Ef6B
vcA3t.bW.tK.2ka3CoXUULGtFpT2GWnYDfP5g.jqB1tZYQm5AfFGF8BtRhdb
y4hSE4pfW3URvSXBSlZ4ZcWvK5JI3IMYOmUU1fUxYNJ5wuJdUE115a0ZRiHM
uTDRX+qtk4HYN.2fjdBNMtosuJVMiYcMPh8hbls3NcM0O5gCdv3B0wZfgVXf
7nyfAFXgAFdFrOkE1m3LXeRKrO1Yv9D1D.4pygEZSHjKOGVnvFK7bTKTvswB
4mCKjYiEdN5pVPsoqlyRaYhMV3YIFZS93fCWFk2bCjayHF1DuOsVnx1pgm7X
nz1pgmbKTXao7I2B41NvvStEZSG1L94vBI11RgcvGt80Q2yLcZ+lN0iMcR+l
NyeM8xFc8X57SqoaSh0yPVKlM4UKR7yO3ytmLfp.Ms.ZM9JVdnMG0cYhxe84
xdHszoogBpAdMwi8Z1H7ZEKz.ul5wdM0dulKMoBdfG6zjQTTKnRC7Zl+50kR
5aqWyHLC7ZtG60g160QgQF3zBO1oGQZqf.kANs7z5zgVlplMjOKDAZzGK0+R
RjaOxaRUGZapZKcZZPH2.ul3wdMaDdsLfXfWS8XulZuWWn01vNcfG6zjQTTy
kAF30L+0qoQivqoBgAdM2i85P685HN0.mV3wN8HRaEPCMvoOwopCrLUMYHel
FTNJLNuj1Bd3ti7lT0A1lp1RmlpTAF30DO1qYivqERgAdM0i8510m6bkvMv1
Dt1VfwzK9y.EXL+0qaG28A7ZhdweFvq4drWGZuWGpWFjAbZgG6ziH4iRuJHC
3zm3Dt1H9pQUuY7.8a1jRh7BCnaOxaJnswmU16yJEw.e1iKmk16yUCsb.eV4
u9L2qx0Zikyj8a5g9qoSsq0ESuvSL41C8lQyZkWKGgWKoLC7ZpG60hQ30L8y
V8.dMyi8ZxH7ZhdoUGvqOwCIzJFnLpcMkTV3FJ0D7KTaOxaZVakSKsvoCXQ0
b5xi7lV0V4zBKbZk90vSkSqnROpQsUNM2BmVDVujt7HuoMsv10f4TS7Fi64O
sFLluafTe2.I9tAZ4RRepaiPi77.HMz2MPe+YBiZ0LYOGOoFTqdrvNGOwPTq
dTMNGOwPTtsqv9IuqFlsqF9I2Bo1tx0mbKzl7czyRaYa0np+PXsKt6Ja+W6b
fsl0dOP46L2AdPxacio4KSebURwtxx8S9kuTeqKn02kF5GCedfpZ0GZ6gJu4
CTdscYkFOL40ewmz8Ch+.a9LsswyTqzquMblt1rYpW32wlLSGavLcu4xL7FK
SWapLM1PYLbyjo1FISjn5c.fFXmvxCCE6uBBctIxXvFHiIadLCtwwX3lFSOa
XLlsYwLvFEyfaRLCtAwLvlCyvaLLCtovXvFBiIaFL1rQvzyl.yfa.L8u4uz+
F+R+a5K8tguz0l8R6azKcrIuXzF7hgatKsuwt7lt0swEl7dBgq2coBzuyR4A
G8qIDwUxFGnvpvmtKVWD9tR13.kRk4gOk9k4nKBehqivGiIMO7IcWsuqs8cw
7LWuT7sL9ElTnNJRIFtQKx6IXxvFs3E0FsHU+RoNTgMZQrQKhMZQrQK1UtoV
+biXmQaxGMdqpP+XCVsyfD3rspBt3VYiA4mMLRWsAETsQK6tcgNNGa3e6sZh
Q5G6BJw0gZJB0MC0UOCxQgNNRyhP2Gs08AqZtXNLRGfcpUi53l57cpUl51bO
VLeBMulYWvuRWHly13x3xayc0uYoO93qESft4FI2jOWMqu7AlKMcO9S+FflV
8hfl3tcUN9M59eYUOTVssWpeX406VMUaIAtoLH.6rec0cjHP53c1Od3UvN6G
21s2lRh98k82Fts6uMs+t+T2Hvu1Nnr20nctGZ4Y6GTba2ZyX9zdaVOUg5v5
8osyp1e0x1W0JeZKghSs054dTrmEMl58di0GLlNjtH1f5XiJI3EQZDlZLsXt
NcMlw6RsUiUTTNzbo9MsQ8Cn5cKZ8OKO33ql6g6IcGi14AUy+2EZmSg14P6b
ncNzNGZmCsyg14P6bHnKzNGZmCsyg14P6bncNzNGZmCsyg14P6bncNzNGZmC
syg14P6bncNzNGZmCsyu.0NWoGosSzNm.syg14P6bncNzNGZmCsyg14PPWnc
NzNGZmCsyg14P6bncNzNGZmCsyg14P6bncNzNGZmCsyg14P6bncNzNGZmeAp
ctjKbk147HncNzNGZmCsyg14P6bncNzNGB5Bsyg14P6bncNzNGZmCsyg14P6
bncNzNGZmCsyg14P6bncNzNGZmCsyg14P67yj14FpVtVrbNgoCZG8lE+gaQ8
W3aV7OlNOKYUxr61rNV2kO6w6MHxRUxvZwVZjgfHH5I3xAHBWTfHnW8XkfBP
D.HB.DA.hfmHiHKPKqkj4X0snDnX6dgZs.VTkxwg5Hni3.n1nGZKy45HFh53
sVG28cmbynIxe4iFWslS0yRip6BW4LMQtYDA7q4ozWt5GVV4V+KgvYwa4sIM
BqSeZwgynn29vq5B2FbIGPsU5Mph2eoJaZwX9+xTKk9VOnQsz2LhvcEFA2lr
grcDMMPCwztkX5UyTO4ZFOzcEGg2PEGhZzfD+b9DqeZTkFUIk2v0M2cr4Pi.
WHckWPnyI6PtPXjq.tPrUpR4khpQ15XEqFgYhFwxGhQIX051uUOkFEGcInAZ
nkwEi0RKRTJelddcUngV+.prZT.jsGcMFuXjKkVH1JFtOAHhZLst8EBKrEKJ
ehJJZzHLdpI8evY7x0BpZxBMm5P0QBstn7cGcIzPy5Xl5RAnF5Xxl3KMCoio
CPuw3UWv8d2yXsNVi2ueyTLd.QDBoqADgA.Q.fH.PD.HB.DA.h..Q.fH.PD.
HB.DA.h..Q.fH.PD.HB.DA.h..Q.fH.PD.HB.DA.h..Q.fH.PD.HB.DA.h..
Q.fH.PDOBPDFm4Z.QH.PD.HB.DA.h..Q.fH.PD.HB.DA.h..Q.fH.PD.HB.D
A.h..Q.fH.PD.HB.DA.h..Q.fH.PD.HB.DA.h..Q.fH.PD.HB.Dwi.DgnoDv
g.hbvjEAfH.PD.HB.DA.h..Q.fH.PD.HB.DA.h..Q.fH.PD.HB.DA.h..Q.f
H.PD.HB.DA.h..Q.fH.PD.HB.DA.h..Q.fH.PD.HxYDPjPhx07gDB9P.eHfO
DvGB3CA7g.9P.eHfODvGB3CA7g.9P.eHfODvGB3CA7g.9P.eHfODvGB3CA7g
.9P.eHfODvGB3CA7g.9P.eHfOD+gODolHDWxGR.3CA7g.9P.eHfODvGB3CA7
g.9P.eHfODvGB3CA7g.9P.eHfODvGB3CA7g.9P.eHfODvGB3CA7g.9P.eHfO
DvGB3CA7g.9PbCeH+TgfBJS1EYBnpZSITPMCBDZOPfnNdHP7i.XXnIAPIgWO
.xN9.n7JI.xkFUCjUsHpUAP9wG.EWIAPVPfQaDTABGG.IWIAPAiYxKJIEq1H
8bP7K5ZH782lXT2eAkZevi1tFWGYrK7ZH14B7L4gDGimInyDzYt2.eAcl5YK
.5LAcl6Wk.zY9NPmIny7BORC5LuPpiC5LGcjFzYB5LulgfBzYdFC9fNSOpv.
zY5UEGfNSuoz.zY5HgxAclfNyA4oAzYB5LAclNy3Acls0+AnyDzYdZMdPmIn
y7DQlTD0.FPTRc+Z7HGQlz0BalJpIjwIpVWCmE9tVHyTJMI7wXNN7wAaWMol
ycrcwn.tK.2Ef6BvcA3t.bW.tK.2Ef6BvcA3t.bW.tK.2Ef6BvcA3t.bW.tK
.2Ef6BvcA3t.bW.tK.2Ef6BvcA3t.bW.tK.2Ef6xM7gTrpJlCWCUp6iKzLBP
H8P.xUAaWsrnS8.PiCidAWIQOt4bwohbUvK7JI3ILgISsbstK3EckD7jlrmy
pzui8BCbTzieU7pJrs02p0jF5WydQZFx5dwsLmHyAvFjzSrowMs8EwpYHqqw
QrWfyr01oqY90xn1LtLcrFXnEFHO5vA27lafAVXfgmA6SYSIbvYnDVZgAdNr
OgMQPA6bXg1DBEzygEJrwBImCKjaaGMmbKjYiEROCc0Hn11R4jagDaaobpsP
djssTN4VHw1RY1Ae31W7MOyzo8a5TO1zI8a5L+0zKq+2ioyOsltEVN6bjXkE
Y4nm3G7Y2S7.UfViQsx.ESpbyQcWnn7Welws2oogBpAdMwi8Z1H7ZEKz.ul5
wdM0dulKMoBdfG6zjQTTKnRC7Zl+50kBAZqWyHLC7ZtG60g160QgQF3zBO1o
GQZqf.kANs7z5zgVlplMjOKDAZfoJW0bIQt8HuIUcnsopszooAgbC7ZhG60r
Q30x.hAdM0i8Zp8dcwJzOrSG3wNMYDE0bYfAdMye8ZZzH7ZpPXfWy8XuNzdu
NhSMvoEdrSOhzVAzPCb5Sbp5.KSUSFxmoA5GOyvRYY4g6NxaRUGXapZKcZpR
EXfWS7XulMBuVHEF30TO1qaeU8OWIbCrMgqsEXL8h+LPAFye851gjc.ulnW7
mA7ZtG60g160g5kAY.mV3wN8HR9nzqBx.N8INgqMZraT0aFWmrgUBxSX.c6Q
dSAsM9rxdeVoHF3ydb4rzdetZnkC3yJ+0m4dUtVarblreSOzeMcpcstzuXAC
XxsG5Mil0JuVNBuVRYF30TO1qEivqY5mHyA7ZlG60jQ30D8RqNfWehGRnUnt
YT6ZJorvMHrb4H3B01i7ll0V4zRKbZkFV7Jmt7HuoUsUNsvBmVFQq4zkG4MM
psxo4V3zhFUuEg9z5px8bDpYLe2.o9tAR7bCjF46FXnuaf99CBAUY6Bbepg4
iJscwnO4Vnv1Ue8jagDaWoz9svZWb2U19u14Aasq8d501YuC7Tq07IVq9i4b
6uJg0q2AummVsNeR0Z7HRV+4xrqmPs2V+McwDUs2GXoO93qEux4a9FAaxmqd
OoOg7I4.AGQj9geToEaiXPzgzdzgx6N5TOf12i93advSNvKSsI6hbCUsRT8x
dT+PPV8HQNtHG6BHxU+0PWxCEutiqE2HeJJ++UudWnXfvGWUozotUIKZ7gO5
EP3iV+Mb4uLIcwKul8koCDizucABpDGkL9HzEP.hW+8u5+Lop50mnLotJV3t
ZWzgpZQBzKEE6XaY58ML2+I1t0WRE5mu8iO+mko+192+vGJ6cQf1F6Rs3vgO
kIGLA3tFQkn43l6sbvZqfYnU7lZDFZCaBYuIFAyFinwajqVVgvyikw51xnuI
VF0pRNwoLnYtow51zdihZVUUieRiZVUWieRiZTahZrSZTiZSTicRiZ1XYs20
Z0I0mo7mZCq71VKwu1LZlv+w4KySuVksc52h2tk9Tj089jU+p321bw1lXhhT
8j4oeTG1Oe+zGWt543rZahYsl8u0Ynje+VkaKYIqtSuuJUavS6MjfpMNihcL
szmy8l56rREt6lSR2dxCGF0GlL893EOUMbJWGE48FEITmGEIWiQQVeQQtd2n
vkQwvqwfHsufHSqGkKChANNHZX7pzhaNc.c3a+NnqBhGNntFKp5.rG2ZAkw2
IpA2olI9m90zYyZr6+sWJz2XigXpwPe6MlPSsE1ausDXpsvOAERbSMFwQYL6
ce5vXzig+ntQMlWWO2msi50UsIL0AYt9F2za5AcJ5QFZaZ88yn0IoLjdXnjd
RJCIt9FaRSUkChrTChrpFelC3QW9Ipp1+SFTrTdZF6BJALr7nizNCMofPnq3
eT2n.SuQri7FoL3FIeKpZY5Ml579kDmpJ0ByqUeb2Hlo0VN15+Tp4UWNtaDw
TWRzxHm2aSLu3lr2lU9daP4Gtoj28FQ99a93ka33ssIiWLWm2+ue++OvNwTW
L
-----------end_max5_patcher-----------

Final Notes

That's all for today! My plan is to do a series of posts, each covering a class of reverb algorithms. For the next one, I'll be writing about rings of allpass filters—this is relevant to, for example, Jon Dattorro's popular 1997 algorithm that appears to be based on a plate reverb from Lexicon's 224 and 480 reverb units. Until next time!

This notation comes from the idea of the Z-transform. ↩︎
Note that the triangle symbol is the standard DSP symbol for amplification/an amplifier. Also note that $b$ and $a$ are often used for feedforward/feedback coefficients, although it seems to be somewhat inconsistent which is which. ↩︎
M. R. Schroeder and B. F. Logan, “‘Colorless’ artificial reverberation,” IRE Transactions on Audio, vol. AU-9, no. 6, pp. 209–214, Nov. 1961, doi: 10.1109/TAU.1961.1166351. ↩︎
M. R. Schroeder, “Natural sounding artificial reverberation,” in Audio Engineering Society Convention 13, Audio Engineering Society, 1961. Accessed: Dec. 29, 2024. [Online]. Available: https://www.aes.org/e-lib/download.cfm?ID=343 ↩︎